排序与搜索

关于作者

大家好，我是翟路佳。全栈工程师，编程爱好者，喜欢分享。

我今年的首要目标是成为一名合格的讲师，帮助尽可能多的同学获得进步。

经常出没于：

• 博客：http://blog.meathill.com
• 微博：https://weibo.com/meathill/
• 我的其它分享 https://github.com/meathill-lecture

冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

1. 假设有一个长度为 N 的数组 arr，需要降序排列
2. 先比较 arr[0] 与 arr[1]，如果 arr[0] < arr[1] 就交换它们的位置
3. 再比较 arr[1] 与 arr[2]，如果 arr[1] < arr[2] 就交换它们的位置
4. 重复2~3，直至对比完所有元素，此时最小值应该处于数组最后
5. 重复2~4，不过每次（第M次）只需要比较到 arr[N-M] 即可
6. 最后数组完成降序排序

完成后的代码如下：

let arr = ['待', '排', '序', '数', '组', ...];

for (let i = 0, len = arr.length - 1; i < len; i++) {
  for (let j = 0, jlen = len - i; j < jlen; j++) {
    if (arr[j] < arr[j + 1]) {
      let tmp = arr[j];
      arr[j] = arr[j + 1];
      arr[j + 1] = tmp;
    }
  }
}

插入排序

假设数组是有序的，那么只需要扫描数组，找到比要插入的数大/小的位置，插入新值，即可。

没有有序数组，那就构建有序数组，即可。

1. 一个数组 arr，需要升序排列
2. 数组第一个值视为已排序，用 arr[1] 与之比较，如果 arr[0] > arr[1]，就把 arr[1] 插入 arr[0] 的前面
3. 此时可以视作前两个值已排序，用 arr[2] 与它们比较，如果有比 arr[2] 大的，就把 arr[2] 插到它前面
4. 重复2~3，直至循环到最后一个数字

JavaScript 表示如下：

for (let i = 1, len = arr.length; i < len; i++) {
  for (let j = 0, jlen = i; j < jlen; j++) {
    if (arr[i] < arr[j]) {
      arr.splice(i, 0);
      arr.splice(j, 0, arr[i]);
      break;
    }
  }
}

从 break 可以看出，插入排序的时间复杂度并不稳定。

• 最好情况，本身是降序数组，改为升序，每次只扫描一个数，结果运算 N - 1 次，即 O(N)
• 最差情况，本身是升序数组，每次都要全扫描，结果运算 (N^2 - N)/2 次，即 O(N²)，和冒泡一样

不过，因为一直在原有数组上操作，所以其空间复杂度是 S(1)。

很多排序算法都有 最好情况 和 最差情况，这也是我们挑选算法和做优化时必须注意的。

二分查找法

对于一段长度为 N 的有序数组 arr，要查找最合适插入 M 的位置

1. 先对比 arr[N / 2]
2. 如果 M < arr[N / 2] 则继续对比 arr[N / 4]；否则，对比 arr[N * 3 / 4]
3. 重复2，直到下一次要对比的集合中只有个1个元素
4. 对比最后的元素，确定位置

二分查找法是最简单的检索方法。它的算法复杂度是 O(logN)。

它的 JavaScript 实现如下：

function find(num, arr) {
  function binarySearch(left, right) {
    if (left > right) {
      return -1;
    }
    if (right - left <= 1) {
      return num > left ? right : left;
    }
    let mid = right + left >> 1;
    if (num <= arr[mid]) {
      return binarySearch(left, mid);
    } else {
      return binarySearch(mid + 1, right);
    }
  }

  return binarySearch(0, arr.length - 1);
}

用 Debug 看一下效果：

./sample/insert.js

使用二分查找法改造插入排序之后，变为：

for (let i = 1, len = arr.length; i < len; i++) {
  let index = find(arr[i], arr.slice(0, i));
  arr.splice(i, 1);
  arr.splice(index, 0, arr[i]);
}

改造之后的“二分查找插入排序”的时间复杂度就变成：

log1 + log2 + log3 + .... + logN ≈ O(NlogN)

它不再有最好情况和最坏情况。

其空间复杂度不变。

堆排序

堆排序是利用“堆”这种数据结构的特性进行排序的算法。

堆可以视作一棵完全二叉树，它满足：

1. 任何节点最多有两个子节点（二叉树）
2. 除了最底层意外，每一层都是满的（二叉树）
3. 任意节点，它的值总是大于/小于它父节点的值（堆）
4. 把它用一维数组表示，任意节点 i 的左节点位置是2i+1，右节点是 2i+2

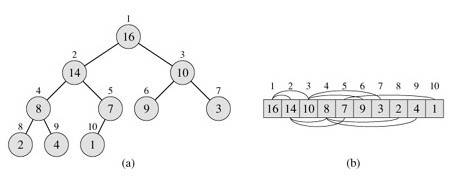
如果有了堆，那么对其排序是很简单的：

1. 取出根节点（最大/最小）
2. 把最后一个节点放到根节点的位置上
3. 调整顺序，使其恢复堆的状态
4. 重复这个过程，直至完成排序

图片来自 精通八大排序算法系列：二、堆排序算法

构造堆

function maxHeapify(arr, index, heapSize) {
  let max = index;
  let left = index * 2 + 1;
  let right = index * 2 + 2;

  let big = right < heapSize && arr[right] > arr[left] ?
            right : left;

  if (big < heapSize && arr[index] < arr[big]) {
    max = big;
  }

  if (max !== index) {
    swap(arr, max, index);
    maxHeapify(arr, index, heapSize);
  }
}

// 从最后一个父节点开始遍历，将其转化为“最大堆”
for (let i = arr.length >> 1; i >= 0; i--) {
  maxHeapify(arr, i, arr.length);
}

排序

for (let i = arr.length - 1; i > 0; i--) {
  swap(0, i);
  maxHeapify(arr, 0, i - 1);
}

堆排序的时间复杂度

因为构建堆和排序是分开的，所以可以分开计算，然后相加。

总复杂度 = 构建堆 + 排序

构建堆：

1. 从 N/2 处开始构建
2. 每个节点最大计算次数是：（总深度 - 节点深度） * 2
3. 每个节点最小计算次数是：2
4. （偷懒省去证明过程）所以时间复杂度是 O(N)

排序：

1. 每次从上到下调整，实际上是 logN
2. 共计 N - 1 次，故为 （N - 1）logN

合并：

(N - 1)logN + N ≈ NlogN

很明显，堆排序的空间复杂度是 S(1)。

归并排序

归并排序是分治法的一种体现。分治法的思路是：把一个大问题分解成若干小问题，分别解决之后再合并回大问题。

这种思路一方面可能降低算法的复杂度；另一方面，把问题分解，可以用有限的资源解决较小的问题，变不可能为可能。

分治法的核心在于分解和合并。

1. 对一个长度为 N 的数组
2. 对每两个相邻的元素进行排序，形成 floor(N/2) 个有序子段
3. 对每两个子段进行归并，形成 floor(N/4) 个有序子段
4. 重复 3 直至归并成一个数组，则这个数组已经完成排序

合并过程：

1. 设定两个指针，分别指向两个子段的一端
2. 把较小的一个元素取出，该指针右移一位
3. 重复2，扫描完毕，得到一个有序子段

function mergeSort(arr) {
  function merge(left, right) {
    let final = [];
    while (left.length && right.length) {
      final.push(left[0] < right[0] ?
          left.shift() : right.shift());
    }
    return final.concat(left, right);
  }

  let len = arr.length;
  if (len < 2) return this;
  let mid = len >> 1;
  return merge(mergeSort(arr.slice(0, mid)),
               mergeSort(arr.slice(mid)));
}

快速排序

快速排序是分治法的另一种体现。

1. 挑一个元素，称为“基准”（pivot）
2. 遍历数组，把小的挪到基准的左边，大的挪到基准的右边
3. 递归的处理两个子数组

我们通常使用“原地排序”（in-place）版本，即选定一个元素，把它移到最左边或最右边，然后遍历数组。或者干脆拿最左边或者最右边的元素作为基准元素。

function quickSort(arr, left, right) {
  let pivot = arr[left];
  let current = left + 1;
  for (let i = current; i <= right; i++) {
    if (arr[i] <= pivot) {
      swap(arr, i, current);
      current++;
    }
  }
  swap(arr, left, current);

  quickSort(arr, left, current - 1);
  quickSort(arr, current + 1, right);
}

最理想的情况下，快速排序的时间复杂度为 O(NlogN)：

1. 每次扫描全部元素，为 O(N)
2. 如果每次都能把数组均分，那么共遍历 logN 次
3. 即 O(NlogN)

最坏的情况下，每次都选到一个边界值，时间复杂度就是 O(N²)（=冒泡）。

那么问题就是如何让数组均分。

一般来说，面对一个很随机的数组，可以取随机数。

生产实践中，数组可能不那么随机，可以考虑“三数取中”。

如果数组很长，可以隔一段取一个，然后对所有取出的值取中。

考虑一种极端情况：一个全部元素都相同的数组。

沿用前面的“单向扫描法”，复杂度会衰弱到 O(N²)。

此时最好用“双向扫描法”，可以恢复到 O(NlogN)：

1. 从数组左侧扫描，遇到 >= pivot，停下
2. 从数组右侧扫描，遇到 <= pivot，停下
3. 交换两个值
4. 继续从左侧扫描，重复 1~2

function quickSort(arr, left, right) {
  let pivot = arr[left];
  let i = current = left + 1;
  let j = right;
  while (i <= j) {
    while(i <= right && arr[i] < pivot) {
      i++;
    }
    while(x[j] > pivot) {
      j--;
    }
    if (i <= j) {
      swap(arr, i, j);
    }
  }
  swap(arr, left, j);

  quickSort(arr, left, j - 1);
  quickSort(arr, j + 1, right);
}

Array.prototype.sort()

用法：

arr.sort([compareFunction]);

其中：

1. compareFunction 可为空，此时，按照“字符比较”排序
2. 否则，以 compareFunction 的结果排序

arr.sort( (a, b) => {
  return a - b;
});

比较函数（compareFunction）的返回值

1. 为负，a 在 b 前
2. 为正，b 在 a 前
3. 为 0，参与比较的元素顺序不变

V8 中的实现

1. 基本上可以认为是快速排序的优化版本
2. 以特定算法对多个值取中间值来建立每次的基准值
   1. <1000，三值取中
   2. >1000，每隔 200+ 取一个，然后取中
3. 对小数组（<10）直接用插入排序
4. 对小分区采用递归，对大分区采用循环，降低递归深度，避免爆栈

内省排序（introsort）

快速排序的效率很高，所以大部分排序算法都在想办法优化它。

内省排序的优化点：

1. 当递归超过一定深度，转为堆排序
2. 使用三值取中来确定基准值

1. 优化一个循环

for (let i = 0; i < 100000000; i++) {
  if (i % 2 === 0) {
    // do something
  }
}

答：

for (let i = 0; i < 100000000; i += 2) {
  // do something
}

2. 有一组任意数字，取 Top3，怎么取最方便？

答案：

最直接的做法是3次遍历，复杂度 O(n) + O(n - 1) + O(n - 2) = O(3n-3)。

最快的应该是堆排序，复杂度 O(n) + 3 O(logN) = O(n + 3 logN)

3. 给一本英语字典，找出所有变位词

（比如 deposit 和 topside）

答案：

假定这本字典里有 N 个单词，我们需要遍历它，并且给予每个单词一个指纹。

比如 meathill = m1e1a1t1h1i1l2 = a1e1h1i1l2m1t1

然后把所有单词按照指纹归档。即可。

概念总结

• 时间复杂度
• 空间复杂度
• 最好情况与最坏情况
• 分治法
• 变量类型转换
• 递归/尾递归

未提及的相关概念

• 排序稳定性
• 睡眠排序
• 猴子排序